最基础的类库项目配置

1
2
3
4
5
6
7

<Project Sdk="Microsoft.NET.Sdk">

  <PropertyGroup>
    <TargetFramework>netcoreapp3.1</TargetFramework>
  </PropertyGroup>

</Project>

多目标框架开发

1
2
3
4
5
6
7

<Project Sdk="Microsoft.NET.Sdk">

  <PropertyGroup>
    <TargetFrameworks>netcoreapp3.1;net45</TargetFrameworks>
  </PropertyGroup>

</Project>

根据编写条件代码以针对每个目标框架进行编译

1
2
3
4
5
6
7
8
9
10
11
12
13

public class MyClass
{
    static void Main()
    {
#if NET45
        Console.WriteLine("Target framework: .NET Framework 4.5");
#elif NETCOREAPP3_1
        Console.WriteLine("Target framework: .NET Core 3.1");
#elif NETCOREAPP
        Console.WriteLine("Target framework: .NET Core x*x");
#endif
    }
}

多目标框架下针对不同框架进行分别引用

多目标平台引用修改前

多目标平台引用修改后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

<Project Sdk="Microsoft.NET.Sdk">

  <PropertyGroup>
    <TargetFrameworks>netcoreapp3.1;net45</TargetFrameworks>
  </PropertyGroup>

  <ItemGroup Condition="'$(TargetFramework)' == 'netcoreapp3.1'">
    <PackageReference Include="Newtonsoft.Json" Version="12.0.3" />
  </ItemGroup>

  <ItemGroup Condition="'$(TargetFramework)' == 'net45'">
    <Reference Include="Newtonsoft.Json" />
  </ItemGroup>

</Project>

不同框架的可选符号

可选项目属性

• GeneratePackageOnBuild
  默认为false，如果更改为true，在生成项目时，visual studio将创建的类库生成NuGet包。
• AssemblyName
  程序集名称。
• RootNamespace
  默认命名空间
• OutputType
  输出类型，主要有WinExe、Exe、Library等。
• PackageId
  NuGet包名称。
• Authors
  软件作者名。
• Company
  公司名称。
• Product
  产品名称。
• Copyright
  版权信息
• Description
  对类库的描述和介绍信息。
• Version
  版本号
• RepositoryType
  仓库类型
• PackageTags
  NuGet包标签

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

<Project Sdk="Microsoft.NET.Sdk">
  <PropertyGroup>
    <TargetFramework>netcoreapp3.1</TargetFramework>   
    <GeneratePackageOnBuild>true</GeneratePackageOnBuild>   
    <AssemblyName>NetCoreSample</AssemblyName>
    <RootNamespace>NetCoreSample</RootNamespace>
    <OutputType>Library</OutputType>

    <!-- NuGet -->
    <PackageId>NetCoreSample</PackageId>
    <Authors>icyrene</Authors>
    <Company>icyrene.cn</Company>
    <Copyright>icyrene.cn</Copyright>
    <Product>hello netcore</Product>
    <Description>this is a test library</Description>
    <Version>1.0.1</Version>
    <RepositoryType>git</RepositoryType>
    <PackageTags>test;netcore</PackageTags>
  </PropertyGroup>
</Project>

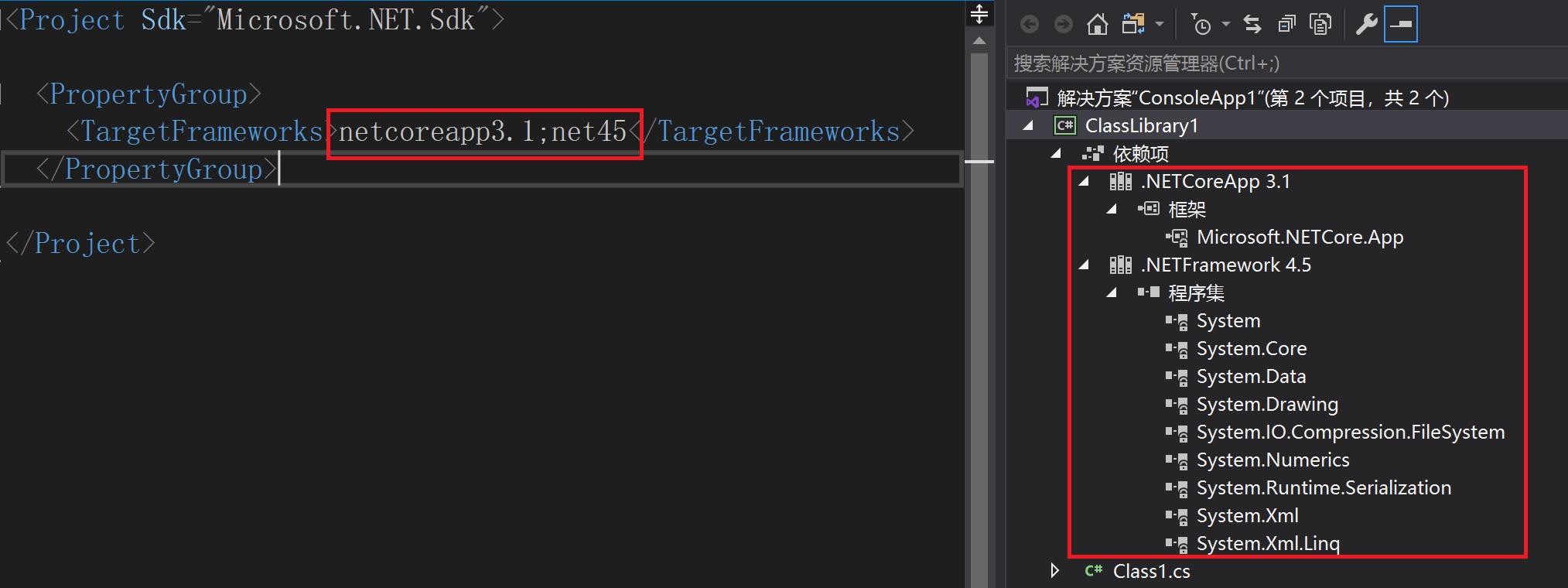
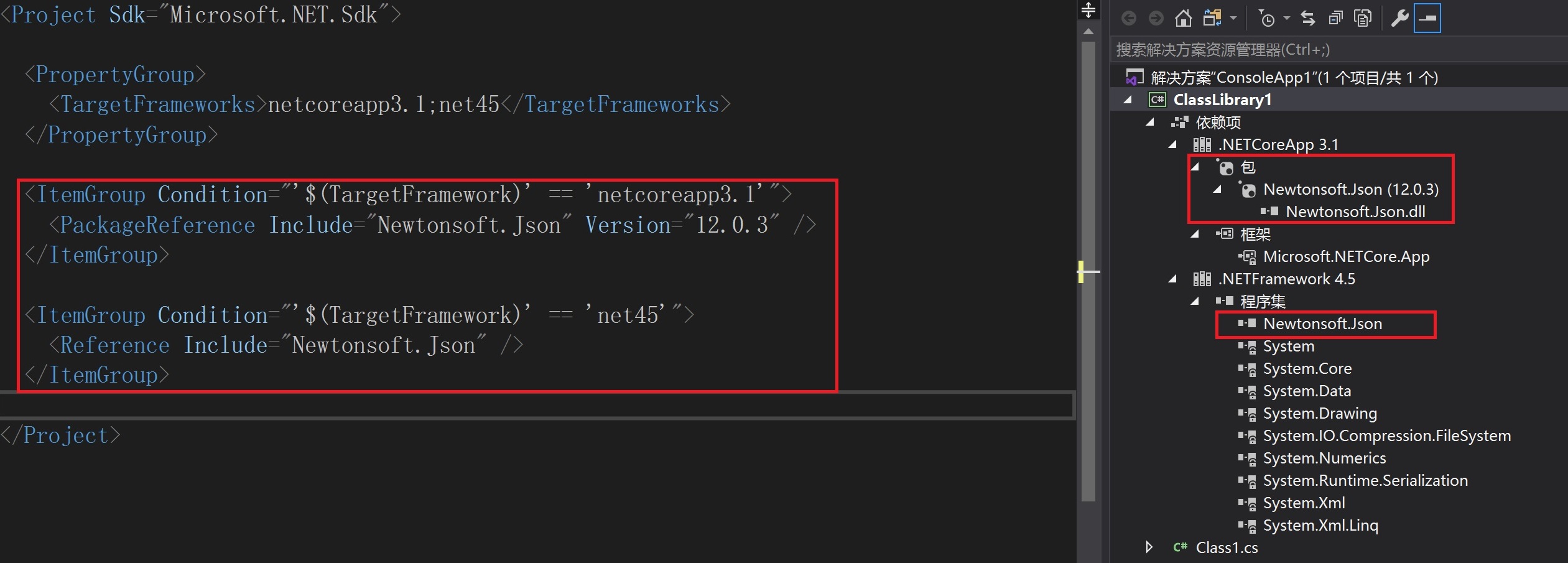
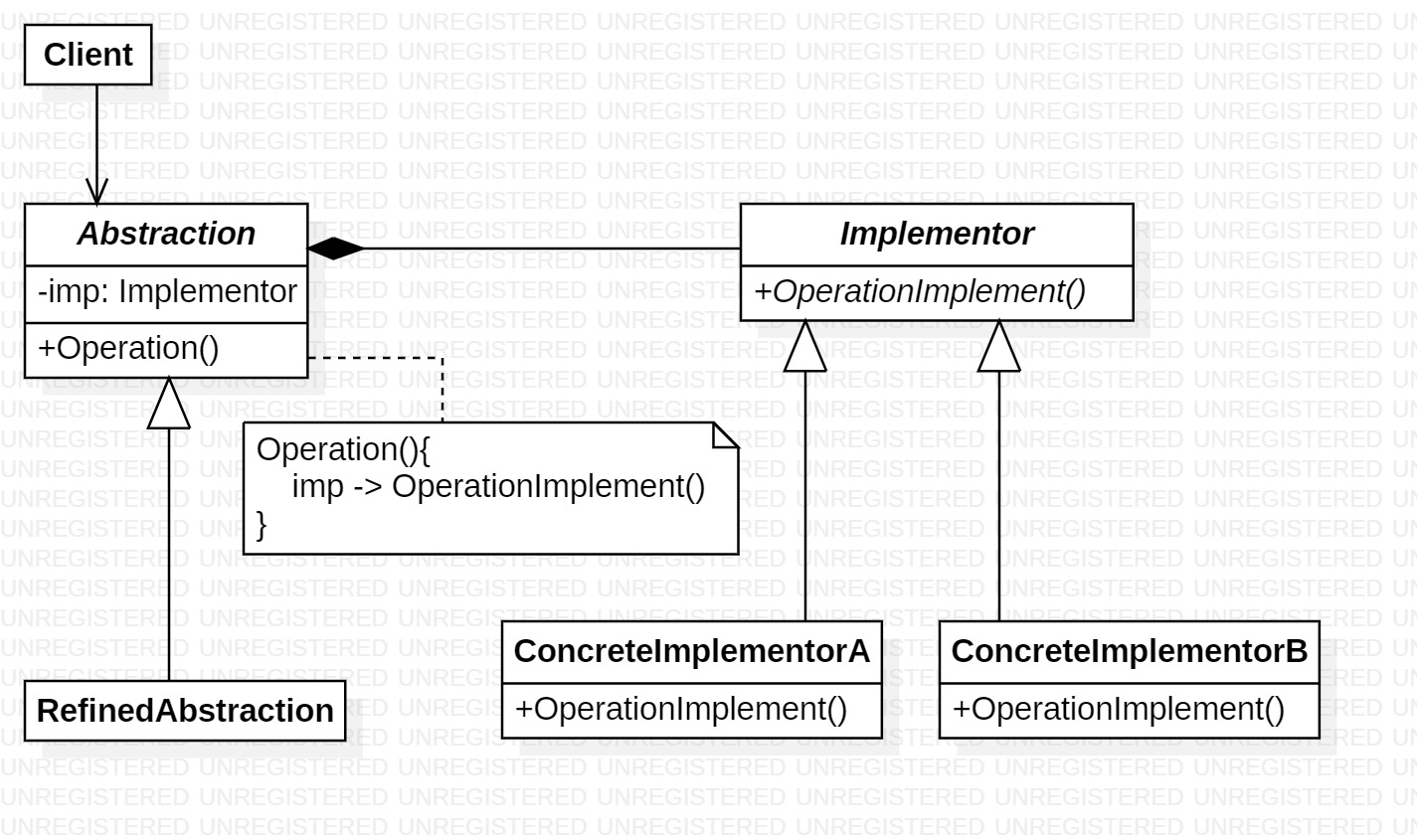
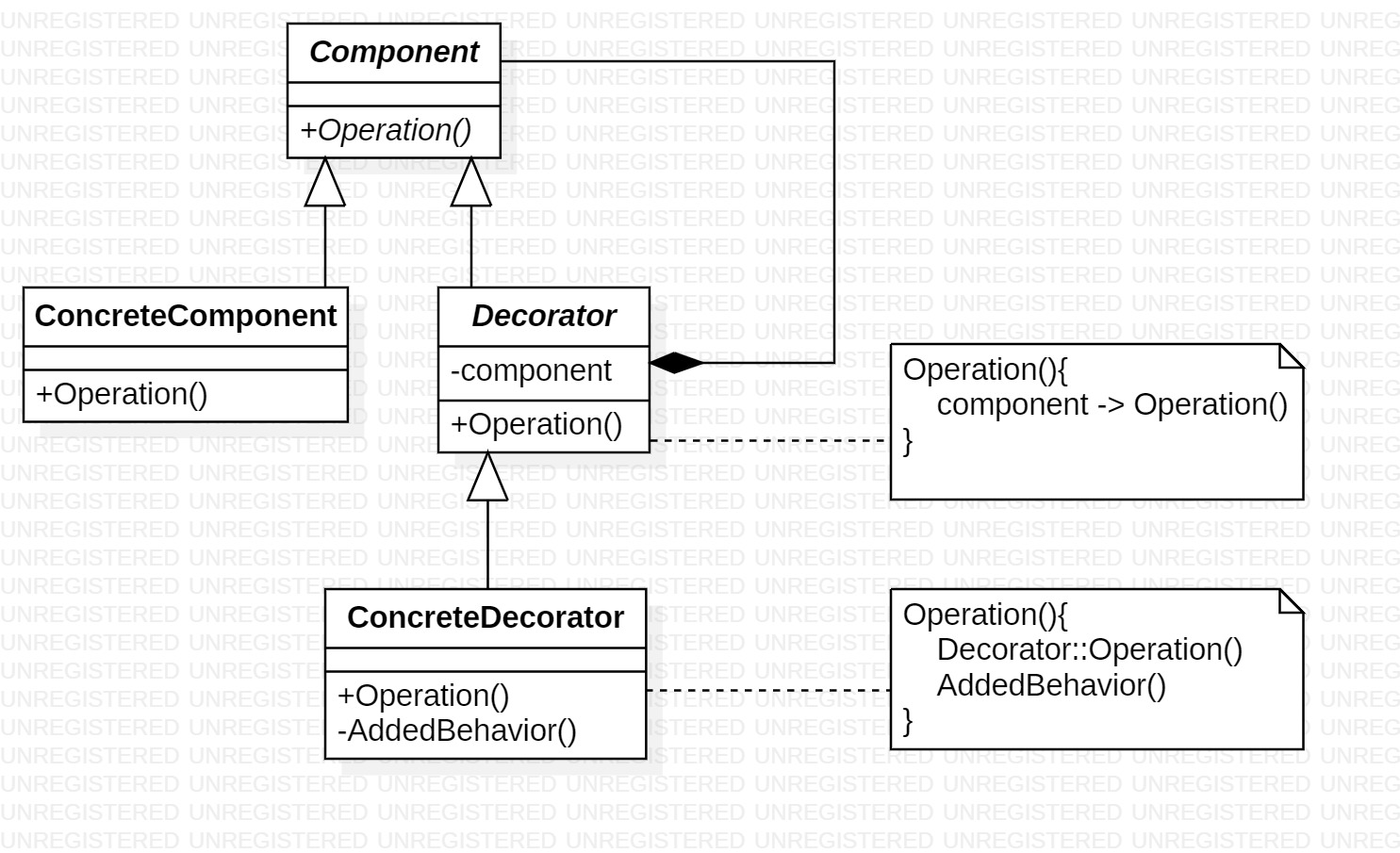
概述

德国物理学家M.普朗克在量子论基础上建立的关于黑体辐射的正确公式。19世纪末，经典统计物理学在研究黑体辐射时遇到了巨大的困难：由经典的能量均分定理导出的瑞利-金斯公式在短波方面得出同黑体辐射光谱实验结果相违背的结论。同时，维恩公式则仅适用于黑体辐射光谱能量分布的短波部分。也就是说，当时还未能找到一个能够成功描述整个实验曲线的黑体辐射公式。

The Planck Function (convert from temperature and wavelength to spectral radiance)

The Planck Function:

$$L(\lambda,t)= \frac{c_1} {\lambda^5(e^{c_2/\lambda t}-1)}$$

Where:

$L(\lambda,t)$=blackbody radiance $(W/m^2 \cdot sr \cdot um)$
$c_1=1.19104210^8(W/m^2 \cdot sr \cdot um^{-4})$
$c_2=1.438775210^4$
$\lambda$=wavelength$(um)$
$t$=blackbody temperature$(K)$

The Planck Function (convert from temperature and wavenumber to spectral radiance)

The Planck Function:

$$ L(v,t)= \frac{c_1v^3}{e^{c_2v/t}-1} $$

Where:

$L(v,t)=$ blackbody radiance $(mW/m^2 \cdot sr \cdot cm^{-1})$
$c_1=1.191042*10^5(mW/m^2 \cdot sr \cdot cm^{-4})$
$c_2=1.4387752(K$ $cm)$
$v=$ wavenumber$(cm^{-1})$
$t=$ blackbody temperature $(K)$

The Inverse Planck Function (convert from spectral radiance and wavelength to temperature)

The Inverse Planck Function:

$$t(\lambda,L) = \frac{c_2}{\lambda\ln(c_1/\lambda^5L+1)}$$

Where:

$t =$ blackbody temperature $(K)$
$L =$ blackbody radiance $(W/m^2 \cdot sr \cdot um)$
$c_1=1.19104210^8(W/m^2 \cdot sr \cdot um^{-4})$
$c_2=1.438775210^4(K$ $um)$
$\lambda=$ wavelength $(um)$

The Inverse Planck Function (convert from spectral radiance and wavenumber to temperature)

The Inverse Planck Function:

$$t(v,L)=\frac{c_2v}{ln(c_1v^3/L+1)}$$

Where:

$t=$ blackbody temperature $(K)$
$L=$ blackbody radiance $(mW/m^2 \cdot sr \cdot cm^{-1})$
$c_1=1.191042*10^5(mW/m^2 \cdot sr \cdot cm^{-4})$
$c_2=1.4387752(K$ $cm)$
$v=$ wavenumber $(cm^{-1})$

特殊字符

限定字符

C#中的使用方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

public static void MatchTest(string input, string pattern)
{
    Console.WriteLine($"--Input--:  {input}");
    Console.WriteLine($"-Pattern-:  {pattern}");
    MatchCollection matchCol = Regex.Matches(input, pattern);
    foreach (var match in matchCol)
    {
        Console.Write($"  {match.ToString()}  ");
    }
    Console.WriteLine();
    Console.WriteLine();
}

public static bool IsMatch(string input, string pattern)
{
    return Regex.IsMatch(input, pattern);
}

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

--Input--:  123456789
-Pattern-:  [^5-6]
  1    2    3    4    7    8    9

--Input--:  123456789
-Pattern-:  [^149]
  2    3    5    6    7    8

--Input--:  123456789
-Pattern-:  [149]
  1    4    9

--Input--:  123456789
-Pattern-:  [2-5]
  2    3    4    5

--Input--:  book,zoom
-Pattern-:  b|zoo
  b    zoo

--Input--:  book,zoom
-Pattern-:  (b|z)oo
  boo    zoo

--Input--:  book,zoom
-Pattern-:  oo
  oo    oo

--Input--:  book,zoom
-Pattern-:  [bok]*
  book            oo

--Input--:  cabbabbabbd,cababd
-Pattern-:  ab*
  abb    abb    abb    ab    ab

--Input--:  cabbabbabbd,cababd
-Pattern-:  (ab)*
      ab        ab        ab                    abab

--Input--:  cabababd,cababd
-Pattern-:  (ab){2}
  abab    abab

--Input--:  cabcabbcabbb
-Pattern-:  ^cab+
  cab

--Input--:  cabcabbcabbb
-Pattern-:  cab+$
  cabbb

创建型设计模式

1. 抽象工厂
2. 生成器
3. 工厂方法
4. 原型
5. 单例

单例（Singleton）

• 定义

  指一个类只有一个实例，且该类能自行创建这个实例的一种模式。

• 特点

  1. 单例类只有一个实例对象
  2. 该单例对象必须由单例类自行创建
  3. 单例类对外提供一个访问该单例的全局访问点

  

工厂方法（FactoryMethod）

• 问题

  在软件构建过程中，经常面临着某个对象的创建工作，由于需求变化，这个对象的具体实现经常面临着剧烈的变化，但是它却有稳定的接口。
  如何应对这种变化？如何提供一种‘封装机制’来隔离出这个易变对象的变化？

• 解决方案

  定义一个用于创建对象的接口，让子类决定实例化哪一个类。Factory Method使得一个类的实例化延迟到子类。 --《设计模式》GoF

  

抽象工厂（AbstractFactory）

• 问题

  在软件构建过程中，经常面临着一系列相互依赖对象的创建工作，由于需求变化，这一系列对象的具体实现经常面临着剧烈的变化，但是它却有稳定的接口。
  如何应对这种变化？如何提供一种‘封装机制’来隔离出这个易变对象的变化？

• 解决方案

  提供一个创建一系列相关或相互依赖对象的接口，而无需指定它们具体的类。 --《设计模式》GoF

  

建造者（Builder）

• 问题

  在软件系统中，有时候面临着“一个复杂对象”的创建工作，其通常由各个部分的子对象用一定的算法构成；由于需求的变化，这个复杂对象的各个部分经常面临着剧烈的变化，但是将它们组合在一起的算法却相对稳定。如何应对这种变化？如何提供一种“封装机制”来隔离出“复杂对象的各个部分”的变化，从而保持系统中的“稳定构建算法”不随着需求改变而改变？

• 解决方案

  将一个复杂对象的构建与其表示相分离，使得同样的构建过程可以创建不同的表示。 --《设计模式》GoF

  

原型（Prototype）

• 问题

  在软件系统中，经常面临着“某些结构复杂的对象”的创建工作；由于需求的变化，这些对象经常面临着剧烈的变化，但是它们却拥有比较稳定一致的接口。如何应对这种变化？如何向“客户程序（使用这些对象的程序）”隔离出“这些易变对象”，从而使得“依赖这些易变对象的客户程序”不随着需求改变而改变？

• 解决方案

  使用原型实例指定创建对象的种类，然后通过拷贝这些原型来创建新的对象。 --《设计模式》Gof

  

结构型设计模式

1. 适配器
2. 桥接
3. 装饰
4. 组合
5. 外观
6. 享元
7. 代理

适配器（Adapter）

• 问题

  在软件系统中，由于应用环境的变化，常常需要将“一些现存的对象”放在新的环境中应用，但是新环境要求的接口是这些现存对象所不满足的。如何应对这种“迁移的变化”？如何既能利用现有对象的良好实现，同时又能满足新的应用环境所要求的接口？

• 解决方案

  将一个类的接口转换成客户希望的另一个接口。Adapter模式使得原本由于接口不兼容而不能一起工作的那些类可以一起工作。 --《设计模式》Gof

• 类图

  两种适配器方式，一种组合方式，一种继承方式，根据面向对象原则，能用组合不用继承。
  

桥接（Bridge）

• 问题

  在很多游戏场景中，会有这样的情况：【装备】本身会有的自己固有的逻辑，比如枪支，会有型号的问题，同时现在很多的游戏又在不同的介质平台上运行和使用，这样就使得游戏的【装备】具有了两个变化的维度——一个变化的维度为“平台的变化”，另一个变化的维度为“型号的变化”。如果我们要写代码实现这款游戏，难道我们针对每种平台都实现一套独立的【装备】吗？复用在哪里？如何应对这种“多维度的变化”？如何利用面向对象技术来使得【装备】可以轻松地沿着“平台”和“型号”两个方向变化，而不引入额外的复杂度？

• 解决方案

  将抽象部分与实现部分分离，使它们都可以独立地变化。 --《设计模式》Gof

  桥模式不能只是认为是抽象和实现的分离，它其实并不仅限于此。其实两个都是抽象的部分，更确切的理解，应该是将一个事物中多个维度的变化分离。

• 类图

  

装饰（Decorator）

• 问题

• 解决方案

• 类图

  

面向对象设计原则

一、开闭原则（Open Closed Principle,OOP）

• 定义

  软件实体应当对对扩展开放，对修改关闭。
  Software entities should be open for extension,but closed for modification.

  这里的软件实体包括以下几个部分：

  1. 项目中划分出的模块
  2. 类与接口
  3. 方法

• 作用

  1. 对软件测试的影响：软件遵守开闭原则的话，软件测试只需要对扩展的代码进行测试就可以，因为原有的测试代码仍然能够正常运行。
  2. 可提高代码的可复用性：粒度越小，被复用的可能性就越大；在面向对象的程序设计中，根据原子和抽象编程可以提高代码的可复用性。
  3. 可以提高软件的可维护性：遵守开闭原则的软件，其稳定性高和延续性强，从而易于扩展和维护。

• 实现方法

  可以通过“抽象约束、封装变化”来实现开闭原则，即通过接口或抽象类为软件实体定义一个相对稳定的抽象层，而将相同的可变因素封装在相同的具体实现类中。

  因为抽象灵活性好，适应性广，只要抽象的合理，可以基本爆出软件架构的稳定。而软件中易变的细节可以从抽象派生来的实现类来进行扩展，当软件需要发生变化时，只需要根据需求重新派生一个实现类来扩展就可以了。

二、里氏替换原则（Liskov Substitution Principle,LSP）

• 定义

  里氏替换原则主要阐述了有关继承的一些原则，也就是什么时候应该使用继承，什么时候不应该使用继承，以及其中蕴含的原理。历史替换原是集成复用的基础，它反映了基类与子类之间的关系，是对开闭原则的补充，是对实现抽象化的具体步骤的规范。

  通俗的讲就是，子类可以扩展父类的功能，但不能改变父类原有的功能。

• 作用

  1. 里氏替换原则是实现开闭原则的重要方式之一。
  2. 它克服了继承中重写父类造成的可复用性变差的缺点。
  3. 它是动作正确性的保证。即类的扩展不会给已有的系统引入新的错误，降低了代码出错的可能性。

• 实现方法

  子类继承父类时，除添加新的方法完成新增功能外，尽量不要重写父类的方法。

  如果通过重写父类的方法来完成新的功能，这样写起来虽然简单，但是整个继承体系的可复用性会比较差，特别是运用多态比较频繁时，程序运行出错的概率会非常大。

  如果程序违背了里氏替换原则，则继承类的对象在基类出现的地方会出现运行错误。这时其修正方法是：取消原来的继承关系，重新设计它们之间的关系。

三、依赖倒置原则（Dependence Inversion Principle,DIP）

• 定义

  高层模块不应该依赖底层模块，两者都应该依赖其抽象；抽象不应该依赖细节，细节应该依赖抽象。

  High level modules shouldnot depend upon low level modules.Both should depend upon abstractions. Abstractions should not depend upon details. Details should depend upon abstractions.

  其核心思想是：要面向接口编程，不要面向实现编程。

  依赖倒置原则是实现开闭原则的重要途经之一，它降低了客户与实现模块之间的耦合。

  由于在软件设计中，细节具有多变性，而抽象层则相对稳定，因此以抽象为基础搭建起来的架构要比以细节为基础搭建起来的架构要稳定的多。这里的抽象指的是接口或者抽象类，而细节是指具体的实现类。

  使用接口或者抽象类的目的是制定好规范和契约，而不去涉及任何具体的操作，把展现细节的任务交给它们的实现类去完成。

• 作用

  1. 依赖倒置原则可以降低类间的耦合性。
  2. 依赖倒置原则可以提高系统的稳定性。
  3. 依赖倒置原则可以减少并行开发引起的风险。
  4. 依赖倒置原则可以提高代码的可读性和可维护性。

• 实现方法

  依赖倒置原则的目的是通过面向接口编程来降低类间的耦合性，所以我们在实际编程中只要遵循以下4点，就能在项目中满足这个规则。

  1. 每个类尽量提供接口或抽象类，或者两者都具备。
  2. 变量的声明类型尽量是接口或者是派生类。
  3. 任何类都不应该从具体类派生。
  4. 使用继承时尽量遵循里氏替换原则。

四、单一职责原则（Single Responsibility Principle,SRP）

• 定义

  单一职责原则规定一个类应该有且仅有一个引起它变化的原因，否则类应该被拆分。

  There should never be more than one reason for a class to change.

  该原则提出对象不应该承担太多职责，如果一个对象承担了太多的职责，至少存在以下两个缺点：

  1. 一个职责的变化可能会削弱或者抑制这个类实现其他职责的能力。
  2. 当客户端需要该对象的某一个职责时，不得不将其他不需要的职责全部都包含进来，从而造成冗余代码或代码的浪费。

• 作用

  1. 降低类的复杂度。一个类只负责一项职责，其逻辑肯定要比负责多项职责简单的多。
  2. 提高类的可读性。复杂性降低，自然其可读性会提高。
  3. 提高系统的可维护性。可读性提高，那自然容易维护了。
  4. 变更引起的风险降低。变更是必然的，如果单一职责原则遵循的好，当修改一个功能时，可以显著降低对其他功能的影响。

• 实现方法

  单一职责原则是最简单又最难运用的原则，需要设计人员发现类的不同职责将其分离，再封装到不同的类或模块中。而发现类的多重职责需要设计人员具有较强的分析设计能力和相关重构经验。

五、接口隔离原则（Interface Segregation Principle,ISP）

• 定义

  接口隔离原则要求程序员尽量将臃肿庞大的接口拆分为更小和更具体的接口，让接口中包含客户感兴趣的方法。

  一个类对另一个类的依赖应该建立在最小的接口上。

  The dependency of one class to another one should depend on the smallest possible interface.

• 作用

  1. 将臃肿庞大的接口分解为多个粒度小的接口，可以预防外来变更的扩散，提高系统的灵活性和可维护性。
  2. 接口隔离提高了系统的内聚性，减少了对外交互，降低了系统的耦合性。
  3. 如果接口的粒度大小定义合理，能够保证系统的稳定性；但是，如果定义过小，则会造成接口数量过多，使设计复杂化；如果定义太大，灵活性降低，无法提供定制服务，给整体项目带来无法预料的风险。
  4. 使用多个专门的接口还能够体现对象的层次，因为可以通过接口继承，实现对总接口的定义。
  5. 能减少项目工程中的代码冗余。过大的接口里面通常放置许多不用的方法，当实现这个接口的时候，被迫设计冗余的代码。

• 实现方法

  1. 接口尽量小，但是要有限度。一个接口只服务于一个子模块或业务逻辑。
  2. 为依赖接口的类定制服务。只提供调用者需要的方法，屏蔽不需要的方法。
  3. 了解环境，拒绝盲从。每个项目或产品都有选定的环境因素，环境不同，接口拆分的标准就不同深入了解业务逻辑。
  4. 提高内聚，减少对外交互。使接口用最少的方法去完成最多的事情。

六、迪米特法则（Law of Demeter,LoD）

• 定义

  只与你的直接朋友交谈，不跟“陌生人”说话。

  Talk only to your immidiate friends and not to strangers.

  如果两个软件实体无法直接通信，那么就不应当发生直接的相互调用，可以通过第三方转发该调用。其目的市降低类之间的耦合度，提高模块的相对独立性。

  迪米特法则中的朋友是指：当前对象本身、当前对象的成员对象、当前对象所创建的对象、当前对象的方法参数等，这些对象同当前对象存在关联、聚合或组合关系，可以直接访问这些对象的方法。

• 作用

  1. 降低了类之间的耦合度，提高了模块的相对独立性。
  2. 由于亲和度降低，从而提高了类的可复用率和系统的扩展性。

• 实现方法

  从迪米特法则的定义和特点可知，它强调以下两点：

  1. 从依赖者的角度来说，只依赖应该依赖的对象。
  2. 从被依赖者的角度说，只暴露应该暴露的方法。

  所以，在运用迪米特法则时要注意以下6点。

  1. 在类的划分上，应该创建弱耦合的类。类与类之间的耦合越弱，就越有利于实现可复用的目标。
  2. 在类的结构设计上，尽量降低类成员的访问权限。
  3. 在类的设计上，优先考虑将一个类设置成不变的类。
  4. 在对其他类的引用上，将引用其他对象的次数降到最低。
  5. 不暴露类的属性成员，而应该提供相应的访问器（set和get方法）。
  6. 谨慎使用序列化（Serializable）功能。

七、合成复用原则（Composite Rules Principle,CRP）

• 定义

  它要求在软件复用时，要尽量先使用组合或者聚合等关联关系来实现，其次才考虑使用继承关系来实现。

  如果要使用继承关系，则必须严格遵循里氏替换原则。合成复用原则同里氏替换原则相辅相成，两者都是开闭原则的具体实现规范。

• 作用

  通常类的复用可分为继承复用和合成复用两种，继承复用虽然有简单和易实现的优点，但它也存在以下缺点。

  1. 继承复用破坏了类的封装性。因为继承会将父类的实现细节暴露给子类，父类对子类是透明的，索引这种复用又称为“白箱”复用。
  2. 子类与父类的耦合度高。父类的实现的任何改变都会倒置子类的实现发生变化，这不利于类的扩展和维护。
  3. 它限制了复用的灵活性。从父类继承而来的实现是静态的，在编译时已经定义，所以在运行时不可能发生变化。

  采用组合或聚合复用时，可以将已有对象纳入新对象中，使之成为新对象的一部分，新对象可以调用已有对象的功能，它有以下优点。

  1. 它维持了类的封装性。因为成分对象的内部细节是新对象看不见的，所以这种复用又称为“黑箱”复用。
  2. 新旧类之间的耦合度低。这种复用所依赖较少，新对象存取成分对象的唯一方法是通过成分对象的接口。
  3. 复用的灵活性高。这种复用可以在运行时动态进行，新对象可以动态地引用与成分对象类型相同的对象。

• 实现方法

  合成复用原则是通过将已有的对象纳入新对象中，作为新对象的成员对象来实现的，新对象可以调用已有对象的功能，从而达到复用。

[TOC]

什么是动态链接库？（Dynamic Link Library,DLL）

动态链接库（Dynamic Link Library）DLL文件与EXE文件一样也是可执行文件，但是DLL也被称之为库，因为里面封装了各种类啊，函数啊之类的东西，就像是一个库一样，存储着很多东西，主要是用来调用的。调用方式主要分为两种：隐式（通过lib文件与头文件） 与 显式（只通过DLL文件）。

C++的入口函数

dll的入口函数，简而言之，就是只在dll被load的时候调用一次，之后都不会被调用，也无法在dll外部被调用。
并且同一个dll，被多个进程load多次，内存中也只会有此动态链接库的一个副本，也只会加载一次入口函数。（由动态链接库的属性决定）

C++的导出函数

• C++的代码示例

1
2
3

//dll.h
extern "C" __declspec(dllexport) int __stdcall Add(int a, int b);
extern "C" __declspec(dllexport) int __stdcall Sum(int* a);

1
2
3
4
5
6
7
8
9
10

//dll.cpp
#include "pch.h"    //预编译头
#include "dll.h"    //头文件

__declspec(dllexport) int __stdcall Add(int a, int b) {
	return a + b;
}
__declspec(dllexport) int __stdcall Sum(int* a){
    return a[0] + a[1] + a[2] + a[3];
}

• __stdcall是函数调用约定的一种，常见的函数调用约定：stdcall cdecl fastcall thiscall naked call,函数调用约定主要约束了两件事：

1. 参数传递顺序
2. 调用堆栈由谁（调用函数或被调用函数）清理

• __stdcall表示

1. 参数从右向左压入堆栈
2. 函数被调用者修改堆栈
3. 函数名(在编译器这个层次)自动加前导的下划线，后面紧跟一个@符号，其后紧跟着参数的尺寸
   在win32应用程序里,宏APIENTRY，WINAPI，都表示_stdcall，非常常见。

• extern “C”

  的主要作用就是为了能够正确实现C代码调用其他C语言代码。加上extern "C"后，会指示编译器这部分代码按C语言（而不是C）的方式进行编译。由于C++支持函数重载，因此编译器编译函数的过程中会将函数的参数类型也加到编译后的代码中，而不仅仅是函数名；而C语言并不支持函数重载，因此编译C语言代码的函数时不会带上函数的参数类型，一般只包括函数名。此处为的是直接将函数名直接导出，在C#调用时不用在单独指明入口点。

  这个功能十分有用处，因为在C出现以前，很多代码都是C语言写的，而且很底层的库也是C语言写的，为了更好的支持原来的C代码和已经写好的C语言库，需要在C中尽可能的支持C，而extern "C"就是其中的一个策略。

  这个功能主要用在下面的情况：

1. C++代码调用C语言代码
2. 在C++的头文件中使用
3. 在多个人协同开发时，可能有的人比较擅长C语言，而有的人擅长C++，这样的情况下也会有用到

• __declspec(dllexport)与__declspec(dllimport)

  他们都是DLL内的关键字，即导出与导入。他们是将DLL内部的类与函数以及数据导出与导入时使用的。

  dllexport是在这些类、函数以及数据的申明的时候使用。用他表明这些东西可以被外部函数使用，即（dllexport）是把 DLL中的相关代码（类，函数，数据）暴露出来为其他应用程序使用。使用了（dllexport）关键字，相当于声明了紧接在（dllexport）关键字后面的相关内容是可以为其他程序使用的。

  dllimport是在外部程序需要使用DLL内相关内容时使用的关键字。当一个外部程序要使用DLL 内部代码（类，函数，全局变量）时，只需要在程序内部使用（dllimport）关键字声明需要使用的代码就可以了，即（dllimport）关键字是在外部程序需要使用DLL内部相关内容的时候才使用。（dllimport）作用是把DLL中的相关代码插入到应用程序中。

  _declspec(dllexport)与_declspec(dllimport)是相互呼应，只有在DLL内部用dllexport作了声明，才能在外部函数中用dllimport导入相关代码。

• 通过DLL Export Viewer 查看生成的导出函数如下所示

  

C#中通过PInvoke调用DLL

通过C#的互操作类可以导入外部函数以供程序调用，调用方式如下所示，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

using System;
using System.Runtime.InteropServices;

namespace PInvokeCSharp
{
    public static class PInvoke
    {
        [DllImport("PInvokeDLL.dll")]
        public static extern int Add(int a, int b);
        [DllImport("PInvokeDLL.dll")]
        public static extern int Sum(int[] a);
        [DllImport("PInvokeDLL.dll")]
        public static extern int Sum(int[,] a);
        [DllImport("PInvokeDLL.dll")]
        public static extern int Sum(IntPtr a);
    }
}

C++与C#中的类型匹配

关于项目

• DataProcess.FileProject 为 Smart里的拼接投影库。
• DataProcess.ProjectTool 为 拼接投影接口工具。
• DataProcess.Gdal 为 GDAL 使用 SWIG生成的 平台调用的源码

如果是新的跨平台项目，PIE.Meteo.Gdal项目可以直接拷贝，里面代码无需修改，也不要修改，如需封装，外加一层封装。

关于开发

关于安装

Linux以CentOS7为例

安装.NetCore环境

注册 Microsoft 密钥和源

1
2
3
4
5
6
7
8

sudo rpm -Uvh https://packages.microsoft.com/config/centos/7/packages-microsoft-prod.rpm


获取https://packages.microsoft.com/config/centos/7/packages-microsoft-prod.rpm
准备中...                          ################################# [100%]
正在升级/安装...
   1:packages-microsoft-prod-1.0-1    ################################# [100%]

安装 .NET Core 运行时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

sudo yum install dotnet-runtime-3.1


=======================================================================================
 Package                    架构      版本        源                              大小
=======================================================================================
正在安装:
 dotnet-runtime-3.1         x86_64    3.1.3-1     packages-microsoft-com-prod     29 M
为依赖而安装:
 dotnet-host                x86_64    3.1.3-1     packages-microsoft-com-prod     39 k
 dotnet-hostfxr-3.1         x86_64    3.1.3-1     packages-microsoft-com-prod    148 k
 dotnet-runtime-deps-3.1    x86_64    3.1.3-1     packages-microsoft-com-prod    2.8 k

事务概要
=======================================================================================
安装  1 软件包 (+3 依赖软件包)

Linux上安装GDAL2.4.0

前期准备，将GDAL安装源码传送并解压到Linux环境中，并安装依赖项

1

sudo yum install gcc gcc-c++ gcc-gfortran.x86_64 byacc.x86_64 flex.x86_64 libjpeg-turbo-devel.x86_64 zlib-devel.x86_64

编译安装 proj-4.9.3

1
2
3
4
5

cd proj-4.9.3
./configure --prefix=/usr/local
make -j4
make install
cd ..

编译安装 geos-3.7.1

1
2
3
4
5

cd proj-4.9.3
./configure --prefix=/usr/local
make -j4
make install
cd ..

编译安装 hdf-4.2.14

1
2
3
4
5

cd hdf-4.2.14
./configure --prefix=/usr/local --enable-shared --disable-fortran
make -j4
make install
cd ..

编译安装 hdf5-1.8.11

1
2
3
4
5

cd hdf5-1.8.11
./configure --prefix=/usr/local
make -j4
make install
cd ..

编译安装 gdal-2.4.0

1
2
3
4
5

cd gdal-2.4.0
./configure --prefix=/usr/local
make -j4
make install
cd ..

配置linux系统的动态库查找目录

1
2

echo '/usr/local/lib' >> /etc/ld.so.conf
ldconfig

Windows上安装GDAL2.4.0

将已经编译好的GDAL解压到Windows64位的电脑上

Path加入以下变量
./gdal/bin
./geos/bin
./hdf4/bin
./hdf5/bin
./jpeg/bin
./proj/bin
./proj/share
./szip/bin
./zlib/bin

加入环境变量GDAL_DATA
./gdal/data

安装处理程序

将生成的程序传送到Linux环境下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

ls

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Config  Data  Debug64  DebugWin64  Release64  ReleaseWin64
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<

cd Debug64/netcoreapp3.1
ls

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Config                            PIE.Meteo.HsdReader.dll
en-US                             PIE.Meteo.ProjectTool.deps.json
HDF.PInvoke.dll                   PIE.Meteo.ProjectTool.dll
libgdalconst_warp.so              PIE.Meteo.ProjectTool.dll.config
libgdal_warp.so                   PIE.Meteo.ProjectTool.exe
libogr_warp.so                    PIE.Meteo.ProjectTool.pdb
libosr_warp.so                    PIE.Meteo.ProjectTool.runtimeconfig.dev.json
PIE.Meteo.FileProject.dll         PIE.Meteo.ProjectTool.runtimeconfig.json
PIE.Meteo.FileProject.dll.config  prjChche
PIE.Meteo.FileProject.pdb         ProjectionSetting.xml
PIE.Meteo.Gdal.dll                Temp
PIE.Meteo.Gdal.pdb                zh-Hans
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<

运行测试程序

1

dotnet PIE.Meteo.ProjectTool.dll FY3D_Project_test.xml

关于调试

通过Visual Studio 使用 SSH 附加到进程 的 方式进行远程调试。

1. 通过宏开关在Debug版本的Program开头加入以下代码

1
2
3
4
5

#if DEBUG   
            //Linux版远程调试附加到进程时使用等待.....
            Console.WriteLine("Please press any Key to continue........");
            Console.ReadKey();
#endif

2. 将Debug版本的输出目录全部复制到Linux远程机器上。
3. 在Linux机器上运行Debug下的主文件，会自动进入等待输入。
4. 打开Windows上的VS,依次展开[调试]->[附加到进程]。
5. 连接类型选择SSH，并加入目标机器。
6. 下侧会出现可用的进程，选择dotnet进程并确定，此时已附加进程成功。
7. 转回到Linux按下任意键，VS将会自动进入断点。

---------------------------------待补充--------------------------------------

概述

MEF,全称Managed Extensibility Framework（托管可扩展框架）。
Managed Extensibility Framework 或 MEF 是一个用于创建可扩展的轻型应用程序的库。 应用程序开发人员可利用该库发现并使用扩展，而无需进行配置。 扩展开发人员还可以利用该库轻松地封装代码，避免生成脆弱的硬依赖项。 通过 MEF，不仅可以在应用程序内重用扩展，还可以在应用程序之间重用扩展。

使用方法

声明以下接口：

1
2
3
4
5
6
7
8
9
10
11
12
13

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace MEFDemo
{
   public interface IBookService
   {
      string BookName { get; set; }
      string GetBookName();
   }
}

实现接口：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.ComponentModel.Composition;

namespace MEFDemo
{
   [Export(typeof(IBookService))]
   public class MusicBook : IBookService
   {
      public string BookName { get; set; }

      public string GetBookName()
      {
         return "MusicBook";
      }
   }
}

调用接口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Reflection;
using System.ComponentModel.Composition;
using System.ComponentModel.Composition.Hosting;

namespace MEFDemo
{
   class Program
   {
      [Import]
      public IBookService Service { get; set; }

      static void Main(string[] args)
      {
         Program pro = new Program();
         pro.Compose();
         if (pro.Service != null)
         {
            Console.WriteLine(pro.Service.GetBookName());
         }
         Console.Read();
      }

      private void Compose()
      {
         var catalog = new AssemblyCatalog(Assembly.GetExecutingAssembly());
         CompositionContainer container = new CompositionContainer(catalog);
         container.ComposeParts(this);
      }
   }
}

Git中的引用 Reference

GIT常用命令

1. 从现有的仓库克隆

1

git clone git://github.com/lx19920404/NoteImages.git

2. 添加文件

1

git add abc.txt

3. 提交更改

1

git commit

4. 进入描述编辑按【i】键,进入输入状态，输入完成后按【ESC】，输入[:wq]回车
5. 推送至仓库

1

git push

6. 撤销提交

   撤销上一次提交

1

git reset --soft HEAD^

撤销前两次提交

1

git reset --soft HEAD~2

7. 从现有工作目录中创建git版本库

1

git init

输出Initialized empty Git repository in D:/…/.git/

8. 将已有分支变基到master并将master快进合并到branch1

1
2
3
4

git checkout branch1
git rebase master
git checkout master
git merge branch1

9. 删除本地分支

1

git branch -d branch1

10. 删除远程分支

1

git push origin --delete branch1

11. 删除远程仓库

1

git remote rm origin

11. 关联远程仓库

1
2

git remote add origin git://github.com/lx19920404/NoteImages.git
git push -u origin master

12. 比较两个版本文件差异，并打包

1

git diff HEAD HEAD^ --name-only | xargs tar -zcvf update.tar.gz

13. 查看当前远程仓库地址

1

git remote show origin

14. 强制推送

1

git push -f origin master

15. 挑拣提交

1

git cherry-pick 9sdsdjksdf #此方法同时也会复制提交时间

16. 二分查找引起报错的提交

1
2
3
4
5
6
7
8
9
10
11

#开始调试 指定终点和起点
git bisect start HEAD f324r23sdf
#调试代码是否正常
#if正常
git bisect good
#else
git bisect bad
#循环调试直至找到开始引起错误的提交
b47892 is the first bad commit
#确定原因后终止调试
git bisect reset

17. 修改git push的默认行为

1
2

git config --global push.default matching #推送所有匹配的分支 
git config --global push.default simple #推送当前分支

GIT瘦身

1
2
3
4
5
6
7
8

# 查看历史大文件
git rev-list --objects --all | grep "$(git verify-pack -v .git/objects/pack/*.idx | sort -k 3 -n | tail -5 | awk '{print$1}')"
# 从历史中删除 target/ 这个文件夹
git filter-branch --force --index-filter 'git rm -r  --cached --ignore-unmatch target/' --prune-empty --tag-name-filter cat -- --all
# 执行仓库压缩
git gc --prune=now
# 推送到远程仓库
git push origin --force --all